在典型的機器學習步驟中，完成 Feature Engineering(特徵工程) -- 從原始資料建立新的特徵後，我們會進行Feature selection(特徵選擇)。

Feature selection 又稱為 variable selection、attribution selection 或 subset selection，它是指從資料集中選出最重要、最相關的特徵來給機器學習建立模型，大部分時候，這樣做可以增加機器學習的效能。

經過特徵工程後的資料，可能還有不相關的資料會導致不佳預測，或有多餘的變數會使學習過程變困難，也可能會導致 overfitting，因此，我們要進行Feature selection 排除這些因素。

Feature selection(特徵選擇)不等於 Dimensionality Reduction(維度降低)，維度降低和特徵選擇累類似，使用非監督演算法降低資料集的特徵數目，但特徵選擇不會改變特徵下資料的內容。

Feature selection(特徵選擇)的程序包括，運用統計等選擇技術，提出一組新的特徵子集合，然後對這子集合做評估。

一般來說，特徵選擇的方法可以分成三類：
Filter methods(過濾器法)
這個方法不會考慮將來要使用哪一種模型進行學習，選擇時只評估變數和預測值的相關，所以它排除最不相關的變數，因為也不會考慮變數之間的關係，所以易於選取多餘重複的變數，然而，這點可以用 FCBF 等演算法來降低這個問題。

Wrapper methods(包裝器法)
Wrapper method 視特徵選擇為搜尋課題(search problem)，然後使用預測性的機器學習演算法來選出最好的特徵子集合。基本上，它是對特徵子集合進行新模型訓練，所以會用到大量電腦資源，然而，它對某些機器學習模型提供學習效能佳的特徵子集合。

Embedded methods(嵌入法)
Embedded method 把特徵之間的關係，以及預期要使用的模型考慮近來，這個方法在進行模型建立的過程同時也做特徵選擇。

1. Filter methods(過濾器法)

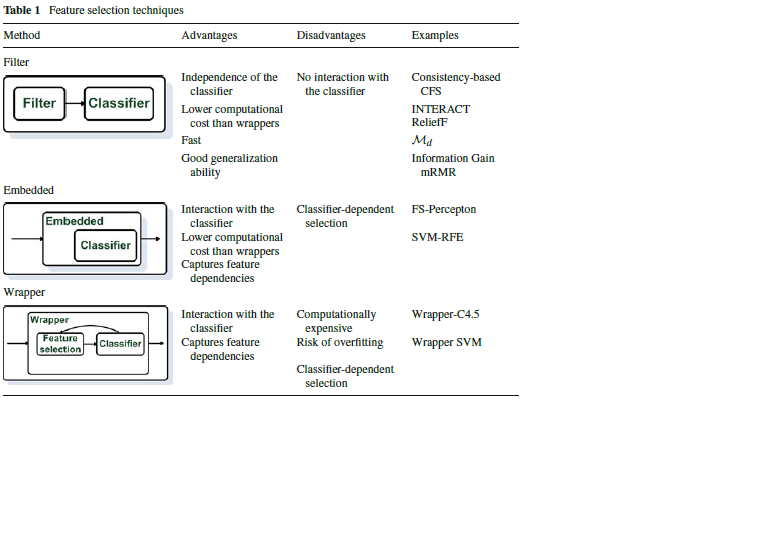
Filter method 以不考慮學習模型觀點從資料集裡選取出特徵。這個方法只考慮變數的特點 所以在開始機器學習前 不合條件的變數會被過濾掉 這個方法能簡單快速 是進行特徵選擇的的第一步

優點：
選出的特徵子集合可以被用在任何機器學習演算法
不會耗費大量電腦資源

型態：
依它處理特徵的方式型態 可分為 Univariate 和 Multivariate 兩種：
Univariate filter methods 根據某些標準依次對一個特徵評估和分級，然後根據標準選擇級數最高的特徵，因為它不會考慮變數間的關係，所以會發生選取多餘的變數。

Multivariate filter methods 評估全部的特徵，它考慮到變數之間的關係。

方法：
1. Basic Filter Methods
2. Correlation Filter Methods
Pearson correlation coefficient(皮爾森相關係數)
Spearman's rank correlation coefficient(斯皮爾曼等級相關係數)
Kendall's rank correlation coefficient(肯德爾等級相關係數)
3. Statistical & Ranking Filter Methods
Mutual Information
Chi-squared Score
ANOVA Univariate Test
Univariate ROC-AUC /RMSE

1. Basic Filter Methods
可以用來移除常數特徵(constant feature)、半常數特徵(quasi-Constant Features)、重複特徵(duplicated Features)。

常數特徵(constant feature) 是一個特徵下的數值都是一樣的，這樣的變數對機器學習模型沒有提供任何資訊。
使用 scikit learning 移除常數特徵

from sklearn.feature_selection import VarianceThreshold
vs_constant = VarianceThreshold(threshold=0)

# fit the object to our data.
vs_constant.fit(x_train)

# 取得常數欄位名稱
constant_columns = [column for column in x_train.columns
                    if column not in 
                    x_train.columns[vs_constant.get_support()]]

# 移除常數欄位
x_train.drop(labels=all_constant_columns, axis=1, inplace=True)             

半常數特徵(quasi-constant features) 特徵下的大部分資料都是同一個數值

# 設定半常數特徵的的門檻
threshold = 0.98

quasi_constant_feature = []

for feature in x_train.columns:

    # 計算比率
    predominant = (x_train[feature].value_counts() /
    np.float(len(x_train))).sort_values(ascending=False).values[0]
    
    # 假如大於門檻 加入 list
    if predominant >= threshold:
        quasi_constant_feature.append(feature)   
        
print(quasi_constant_feature)

# 移除半常數特徵
x_train.drop(labels=quasi_constant_feature, axis=1, inplace=True)

重複特徵(duplicated features)

# 轉置特徵矩陣
train_features_T = x_train.T

# 列印重複欄位
print(train_features_T.duplicated().sum())

# 選取重複欄位名稱
duplicated_columns = 
train_features_T[train_features_T.duplicated()].index.values

# 移除重複欄位
x_train.drop(labels=duplicated_columns, axis=1, inplace=True)

2. Correlation Filter Methods
除了重複特徵外，一個資料集還可能有相關特徵(correlated features)。

Correlation(相關)是衡量兩個變數之間的線性關係，也就是一個變數依賴另一個變數的程度。

假如兩個特徵高度相關，對於我們要預測的標的(target)來說，他們提供了重複的資訊，因為我們只取其中一個特徵就可以做出正確的預測了。所以移除其中一個特徵，不只能降低資料及維度(dimensionality)還可排除雜訊(noise)。

常用到的衡量方法:
Pearson correlation coefficient(皮爾森相關係數)
機器學習常用的方法，是衡量兩個資料變數之間線性關係的強度，它的值介於 1 和 －1 之間

• 1 表示正相關： 當一個變數的值增加，另一個變數的值也增加。
• －1 表示負相關： 當一個變數的值減少，另一個變數的值也減少。
• 0 表示沒有線性相關存在兩個變數之間。

皮爾森相關係數假設：兩個變數是常態分布，兩個變數間有直線關係存在，資料是平均分配在回歸線周圍。

公式：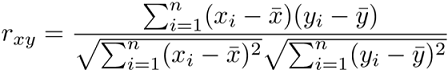

Spearman's rank correlation coefficient(斯皮爾曼等級相關係數)
當兩個變數的關係是非線性相關的，這時就會用到斯皮爾曼等級相關係數。

它是屬於非參數檢定(nonparametric test)，它用單調函數(monotonic function)來衡量兩個變數相關程度，它的值介於 1 和 －1 之間。
當兩個變數完全單調相關時，斯皮爾曼等級相關係數則為1 或 －1。它類似皮爾森相關係數，但是皮爾森相關係數衡量線性關係，而斯皮爾曼等級相關係數衡量單調關係(不論線性與否)。

斯皮爾曼等級相關係數適用適用於連續型(continuous)或不連續型(discrete)有序變數。它也不對變數分布做假設。

公式：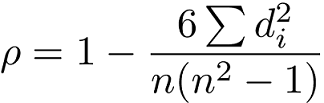

Kendall's rank correlation coefficient(肯德爾等級相關係數)
是屬於非參數檢定(nonparametric test)，用於測量兩個變數順序相關強度。

肯德爾相關係數的範圍在-1到1之間，當τ為1時，表示兩個變數擁有相似的等級相關性；當τ為-1時，表示兩個隨機變數擁有完全不同的等級相關性；當τ為0時，表示兩個隨機變數是相互獨立的。

肯德爾等級相關係數適用適用於不連續型(discrete)資料。

公式：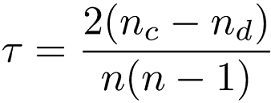

程式範例：

corr_features = set()

# 建立相關矩陣
corr_matrix = x_train.corr()

for i in range(len(corr_matrix .columns)):
    for j in range(i):
        if abs(corr_matrix.iloc[i, j]) > 0.8:
            colname = corr_matrix.columns[i]
            corr_features.add(colname)
            
x_train.drop(labels=corr_features, axis=1, inplace=True)

corr()函數有一個參數method，讓我們指定要使用哪一種相關係數，它的預設值是pearson，可更改為kendall或spearman。

3. Statistical & Ranking Filter Methods
是使用統計測試值來評估每一個特徵，也就是評估一個變數在區別標的(target)上的重要性。

Mutual Information
是測量兩個變數的相依性，也就是我們可以經由了解一個變數來得到另一個變數的資訊。

在機器學習上，Mutual Information測量一個變數對於做出正確的預測Y值提供了多少資訊。

假如X和Y是獨立的，則他們的MI是0。假如X對Y有決定性的作用 則X的熵(entropy)就是MI。在資訊理論中，熵(entropy）是衡量一個變數中包含的資訊量。

公式：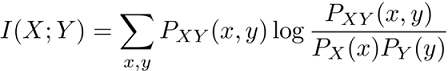

from sklearn.feature_selection import mutual_info_classif
from sklearn.feature_selection import SelectKBest

# 選擇要保留的特徵數
select_k = 10

selection = SelectKBest(mutual_info_classif, k=select_k).fit(x_train, y_train)

# 顯示保留的欄位
features = x_train.columns[selection.get_support()]
print(features)

Chi-squared Score
這個方法只適用於類別變數和二元標的(binary targets)，且變數不能是負數。它比較資料集的特徵和標的變數的關係。

from sklearn.feature_selection import chi2
from sklearn.feature_selection import SelectKBest

# 選擇要保留的特徵數
select_k = 10

# 使用 chi2 score
selection = SelectKBest(chi2, k=select_k).fit(x_train, y_train)

# 顯示保留的欄位
features = x_train.columns[selection.get_support()]
print(features)

ANOVA Univariate Test
ANalysis Of VAriance 簡稱ANOVA，是單變項檢定(univariate test)。和前一個方法
類似，它衡量兩個變數的相依性。

ANOVA假設變數和標的之間存在著線性關係，且變數是呈現常態分布。

這個方法適用於連續型變數和二元標的(binary targets)，但sklearn擴展到適用於回歸問題上。

from sklearn.feature_selection import f_classif
from sklearn.feature_selection import SelectKBest

# 選擇要保留的特徵數
select_k = 10

selection = SelectKBest(f_classif, k=select_k).fit(x_train, y_train)

# 顯示保留的欄位
features = x_train.columns[selection.get_support()]
print(features)

Univariate ROC-AUC /RMSE
使用機器學習模型來衡量兩個變數的相依性，適用於各種變數，且沒對變數的分布做任何假設。

回歸性問題使用RMSE，分類性問題使用ROC-AUC。

步驟：
用一個變數和標的建立決策樹。
根據模型的ROC-AUC或RMSE對特徵做分級。
選取級數最高的特徵。

from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_auc_score

# ROC的分數
roc_values = []

# 計算分數
for feature in x_train.columns:
    clf = DecisionTreeClassifier()
    clf.fit(x_train[feature].to_frame(), y_train)
    y_scored = clf.predict_proba(x_test[feature].to_frame())
    roc_values.append(roc_auc_score(y_test, y_scored[:, 1]))

# 建立Pandas Series 用於繪圖
roc_values = pd.Series(roc_values)
roc_values.index = X_train.columns

# 顯示結果
print(roc_values.sort_values(ascending=False))

結論：
在特徵選取過程中，我們通常先用過濾器法來刪掉不相關(irrelant)，重複(duplicated)，(變數間高度)相關(correlated)和常數(constant)特徵。